In one of the previous articles, we've seen how to define a basic function with if-else expressions. In this article, we are going to get through the detailed overview of defining efficient functions and developing intuition to solve problems in the way of functional programming.

If you already haven't read my previous blogs in this series, I strongly recommend you go and give them a read. Those will help you get a structured idea of how things are different and how expressions work in OCaml.

Without wasting time Let's open utop & directly head towards the topic.

Functions

Defining Functions

See below - a normal function definition.

let is_positive n = if n > 0 then true else false;;
(* In OCaml, function definitions don't contain any return statement.
   While in many imperative languages like - C, Java, C++, they do *)
val is_positive : int -> bool = <fun>   (* utop output *)

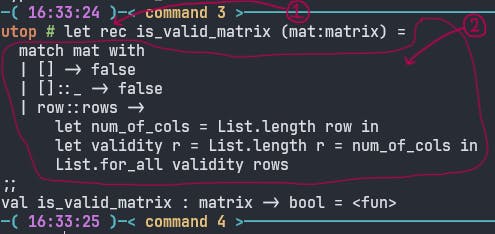
You can see above there is an example of a recursive function in OCaml. From the image, we understand -

1. Recursive functions are defined with adding a rec keyword just after the let keyword.

2. Let it be recursive or any normal function, the whole chunk of code at the right-hand side of the = (equal) sign, always is an expression. Whatever this expression evaluates is the return value. Hence, no return statement required.

There are always consequences of your decisions...

Calling Functions

The syntax for calling any function in OCaml is entirely different from your experience in some imperative or multi-paradigm languages, such as - Java, Python, JavaScript, C++, etc.

# Defining a function in python
def is_positive(x):  # argument `x` inside parenthesis `()`
    if x > 0:
        return True  # return statement
    else:
        return False # return statement

# Calling it
is_positive(20)

In those languages, you place parenthesis after the function name and pass arguments inside that parenthesis. We don't do that here in OCaml. Here, all arguments are passed one after the another based on the sequence or labels(as defined) separated by spaces.

(* Defining a function in OCaml *)
let is_negative n =
  if n < 0 then
    true
  else
    false
;;
val is_negative : int -> bool = <fun> (* utop output *)
(* Calling it *)
is_negative (-50);; (* grouping the value inside parenthesis because it 
                       contains a sign. Otherwise the compiler will 
                       misunderstand `is_negative` as an integer expression
                       instead of a function and as a result, will throw
                       an error.
                     *)
- : bool = true  (* utop output *)

Example of a function taking multiple arguments.

(* A function that computes sum of 2 integers & returns it as a string *)
let string_sum (num1:int) (num2:int) = 
    string_of_int (num1 + num2);;  
val string_sum : int -> int -> string = <fun> (* utop output *)

The functions that take more than 1 argument, are called curried functions. What does it mean? Let's learn that first.

Currying

Currying is a technique used in functional programming to transform a function that takes multiple arguments into a sequence of functions that take one argument each. This allows you to partially apply arguments to a function, creating new functions of fewer arguments. In OCaml, you can easily implement currying using lambda expressions or by defining a separate function.

Let's consider a simple function that adds two numbers:

let add x y = x + y;;
val add : int -> int -> int = <fun> (* utop output *)

In this case, add is a function that takes two arguments, x and y, and returns their sum. Now, we can curry this function to create a sequence of functions that take one argument each:

let curried_add = add;;
val curried_add : int -> int -> int = <fun>   (* utop output *)

curried_add 1;;
- : int -> int = <fun>    (* utop output *)

let curried_add_one = curried_add 1;;
val curried_add_one : int -> int = <fun>    (* utop output *)

curried_add 1 2;;
- : int = 3    (* utop output *)

(* same thing would be below *)

curried_add_one 2;;
- : int = 3    (* utop output *)

So basically, in OCaml, each & every function takes exactly one argument.

Lambda Expressions

Lambda expressions, also known as anonymous functions, are widely used in OCaml. They allow you to define functions without assigning them to a specific name.

Learn the syntax with a basic example of using lambda expressions in OCaml:

(* Non-lambda function finding square of a number *)
let square x = x * x;;
val square : int -> int = <fun> (* utop output *)
(* Lambda Function doing the same thing *)
fun x -> x * x;;
- : int -> int = <fun> (* utop output *)

See below a good example of a lambda expression as an argument passed to a function that takes a function as an argument.

(* map is a function defined in the List module that applies a function
   given as 1st argument to each of the elements of the list given as 
   the 2nd argument & return the resulting list. *)
List.map (fun x -> x * x) [1; 2; 3];;
- : int list = [1; 4; 9] (* utop output *)

So, what about those lambda expressions that returns something independent of any argument or frankly speaking, a lambda expression that doesn't take any arguments?

Exactly, you're thinking absolutely correct. We'll provide unit () to that function as argument.

fun () -> print_endline "I entered the void btw";; 
- : unit -> unit = <fun> (* utop output *)

Recursion

Recursion, in the context of programming, refers to a technique where a function calls itself repeatedly until a specific condition is met. This process allows you to solve complex problems by breaking them down into smaller, more manageable subproblems.

In functional programming, these subproblems are handled with small functions defined at different local scopes or some pattern matching expressions. Pattern Matching is a crucial concept in many functional programming Languages. OCaml is not any exception here. We are getting into pattern matching later.

(* Recursive Function to calculate the nth fibonacci sequence term *)
let rec fib n =
  let rec helper n previous current = (* Implementing a tail recursion with the helper function to make the function efficient & less prone to stack overflows *) 
    if n = 1 then current
    else helper (n - 1) current (previous + current)
  in
  if n > 0 then helper n 0 1
  else raise (Invalid_argument "n must be greater than 0");; (* Handling Exceptions so that we don't get errors *)

The above function has a helper function defined in a lower scope that can't be accessed outside of the function fib definition. This function could be written in a more efficient way. And that way would be involving match expressions.

Solving Problems

If you're not familiar with writing useful programs in functional programming languages, you should know that every single step to solve a problem or make some meaningful program involves a function.

Just like the procedures in an object-oriented language like Java involve implementing Classes, Objects and Methods; OCaml as a functional language, involve implementation of pure functions with strong emphasis on immutability.

Although OCaml is not a purely functional language (it has loops, classes) but it still strongly supports the principles of functional programming.

Let's try to solve a problem in OCaml with some functions.

(* Write a program to calculate the sum of the integer list elements *)
(* Defining the function *)
let rec sum_list lst = 
  if lst = [] then 0  (* base case *)
    (* List.hd takes 1st element & List.tl takes list of rest of the elements *)
  else List.hd lst + sum_list (List.tl lst) (* recursively calling the function *)
;;
val sum_list : int list -> int = <fun> (* utop output *)

(* Calling the function to perform the sum on the list *)
Printf.printf "%d\n" (sum_list [1;4;5;6;9;9;55]);;
89                            (* utop *)
- : unit = ()                (* output *)

Note that this function is not implemented with a match expression. Let's first learn this and then we will solve the same problem again with pattern matching technique.

Pattern Matching

We match different patterns of an argument or its specification to handle all different possible cases of a recursive function. Let's see how that works.

In OCaml, pattern matching is typically performed using the match keyword.

(* Basic syntax of pattern matching *)
match expression with
| pattern1 -> expression1
| pattern2 -> expression2
| pattern3 -> expression3
...
| _ -> default_expression
;;

Pattern Matching in OCaml involves comparing input data against a set of predefined patterns to determine which pattern best matches the input. When a match is found, the corresponding actions or expressions are executed. Pattern matching is not limited to simple values but can also be applied to more complex data structures like tuples, lists, and even user-defined types.

Basic Example

(* computing factorial with match expression *)
let rec factorial n = 
    if n >= 0 then
        match n with
        | 0 -> 1
        | _ -> n * factorial (n - 1) (* `_` is the wildcard character.
                                        It can be anything! *)
    else
        failwith "Only non-negative integers are supported!" (* Error Handling *)
;;
val factorial : int -> int = <fun> (* utop output *)

factorial 5;;
- : int = 120  (* utop output *)
factorial (-5);;
Exception: Failure "Only non-negative integers are supported!". (* utop output *)

We can write the same function implementing pattern matching without the match keyword. Yes! That would be the function keyword. Example will make it crystal clear.

(* Without error handling *)
let rec factorial = function
    | 0 -> 1
    | n -> n * factorial (n - 1);;
val factorial : int -> int = <fun>  (* utop output *)
(* With Error Handling *)
let rec factorial = function
    | 0 -> 1
    | n -> 
        if n >= 0 then 
            n * factorial (n - 1) 
        else
            failwith "Only non-negative integers are supported!";;
val factorial : int -> int = <fun>  (* utop output *)

Advanced Patterns

Tuple Patterns:

let get_first_element tuple =
  match tuple with
  | (x, _) -> x
;;
val get_first_element : 'a * 'b -> 'a = <fun>  (* utop output *)

List Patterns:

let rec sum_list lst =
  match lst with
  | [] -> 0
  | head :: tail -> head + sum_list tail
;;
val sum_list : int list -> int = <fun>   (* utop output *)

Constructor Patterns (for algebraic data types):

type color = Red | Green | Blue;; (* Defining a variant type *)
type color = Red | Green | Blue    (* utop output *)

let color_to_string c = 
  match c with
  | Red -> "Red"
  | Green -> "Green"
  | Blue -> "Blue"
;;
val color_to_string : color -> string = <fun>   (* utop output *)

Record Patterns:

type person = { name : string; age : int };;
type person = { name : string; age : int; }    (* utop output *)

let is_adult (p:person) =
  match p with
  | { name = _; age = a } when a >= 18 -> true
  | _ -> false;;
val is_adult : person -> bool = <fun>   (* utop output *)

Now as you know how to write patterns to handle all important cases, let's rewrite the function to calculate nth Fibonacci number using a match expression.

(* Fibonacci using pattern matching *)
let fib n =
  let rec helper n prev curr =
    match n with
    | 0 -> prev
    | 1 -> curr
    | _ -> helper (n - 1) curr (prev + curr)
  in
  if n < 0 then
    raise (Invalid_argument "fibonacci: n must be a non-negative integer")
  else
    helper n 0 1;;
val fib : int -> int = <fun>     (* utop output *)

fib 100;;
- : int = 3736710778780434371    (* utop output *)

You can clearly see that the above implementation of Fibonacci number generator is not any ordinary one because it itself isn't recursive. The helper function it uses is recursive. It is a highly optimized function which is less susceptible to Stack Overflows.

This approach ensures that the function can be optimized by the OCaml compiler to use constant stack space.

This is how you can implement efficient, highly performant & powerful functions by combining Pattern Matching with tail call optimization.

Best Practices and Performance Considerations

While pattern matching offers numerous benefits, it's essential to use it judiciously to ensure code readability and performance. Some best practices to consider include:

1. Use pattern matching when the structure of the data is known or can be inferred from the problem context.

2. Break down complex patterns into smaller, more manageable patterns to improve code readability.

3. Avoid using overly specific patterns that might limit the flexibility of your code.

4. Be mindful of performance when working with large data structures or deeply nested patterns, as pattern matching can have a higher time complexity compared to other operations, based on the situation.

Conclusion

I hope you enjoyed this article this far.

If this piece of content added a value to your time & energy, please consider giving some likes to this blog and share with others.

Happy Coding! 🧑🏻‍💻 👩🏻‍💻